A Bayesian quest to find God

Bayes’ theorem and the probabilistic answers to the most fundamental question of all: “Does God exist?”

This article focuses not on formula and numbers, but a fascinating story where Bayes’theorem establishes itself across the most controversial discussions in philosophy, epistemology and religions.

We Data Scientists and Statisticians love Bayes’ theorem.

A seemingly simple idea: we get updated and improved belief by updating our initial belief with newly acquired information, Bayes’ theorem has been touted as one of the most powerful method for generating knowledge.

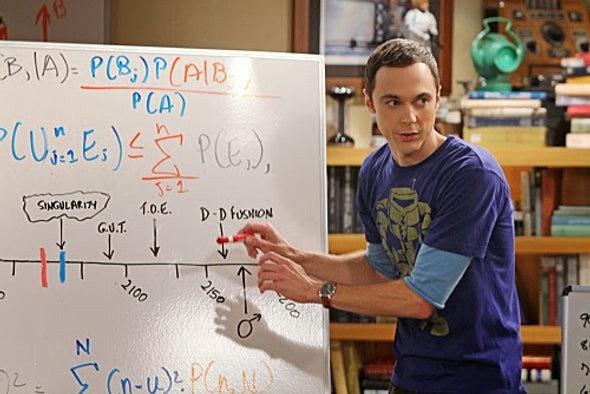
Sheldon explaining how he is estimating his life expectancy, using Bayes’s theorem. Image Source: Scientific America

Alan Turing used Bayes to break Enigma — the Germany navy’s secret codes. We use Bayesian programs to whisk spam emails into junk bins (“Naive Bayes, anyone?”), assess our medical records, discovers how genes are controlled and regulated, assisted Coast guards and homeland security, etc.^[1] It is so popular that it even made a guest appearance on The Big Bang Theorem.

With such rich practical applications, it came as no surprise that philosophers and theologians have found Bayes’s Theorem a new framework to establish a novel theoretical underpinnings for a old, yet ever-inflammatory questions:

Can we make rational conclusions about God based on evidence about the world around us?

1. Bayes’ theorem — A recap:

Bayes’ Theorem is stunningly simple. It is concerned with the conditional probability, that is, the probability that a theory or a hypothesis is true of some event has happened.

The idea is captured in a (in)famous equation:

$$P(X|Y) = \frac{P(X \cap Y)}{P(Y)} = \frac{P(Y|X)P(X)}{P(Y|X)P(X) + P(Y|X^C)P(X^C)}$$

I don’t want to waste your time laboring on this equations. In fact, I have written extensively about Bayes’ theorem and how to make inference the Bayesian way. You can check it out at:How Bayesian statistics convinced me to hit the gym

What I want to do next is to give a motivating example to demonstrate the vast predictive insights of this elegant formula.

Adam is (probably) the first person to use Bayes’s Theorem

Imagine somebody who emerges into our beautiful world (Adam or who he came from Plato’s cave) and sees the sun rise for the first time. At first, he would think of the appearance as some freak occurrence. However, each day that he survives and observes the beautiful sunrise, his confidence increases that it is a permanent feature of nature. How does this mental process of inference — usually referred to as Induction — take place?

There are two events that are of interests:

The sun rises everyday ($X$)
The sun rises today ($Y$)

What Adam cares about, is the conditional probability that the sun rises everyday, given the observation that it rises today $P(X|Y)$. Now, let us assign some number to illustrate the calculations:

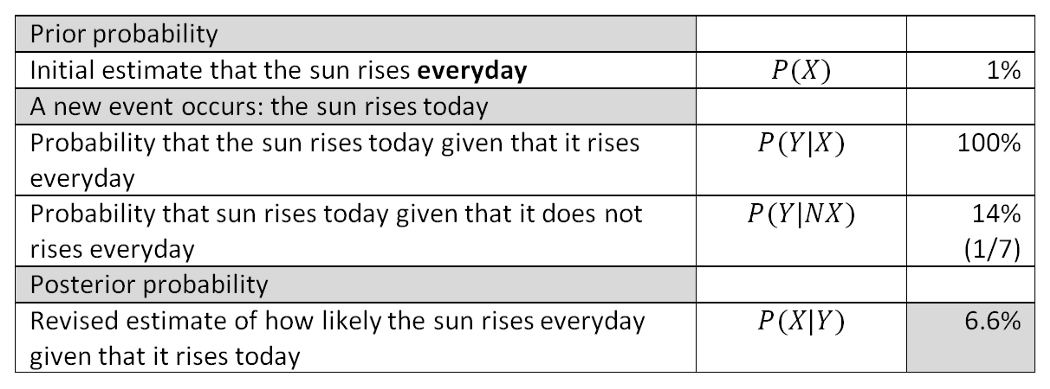
How Adam arrived at the conditional probability after the first sunrise

Let’s say that before seeing the sunrise for the first time, Adam is incredulous and assigns a probability of merely 1% to the hypothesis that the sun rises everyday $P(X)$. As he sees the sunrise, he is not convinced so he assigns a reasonable chance that the sunrise today is purely coincidental (i.e., $P(Y|X^C) = \frac{1}{7}$ as there are 7 days of the week, but it could really be 1/30, 1/365 or 1/1000000). And if Adam knew and used Bayes’ Theorem to run these numbers, the probability he’d assign to the initial hypothesis increases from 1% to 6.6%.

The ingenuity of Bayes’ Theorem is that we can update our probabilistic estimate multiple times as more evidence comes. As Adam wakes up everyday and marvels at the magnificent sunrise, he constantly updates his priors, reruns the Bayesian formula, and gets the updated estimate of conditional probability for his hypothesis:

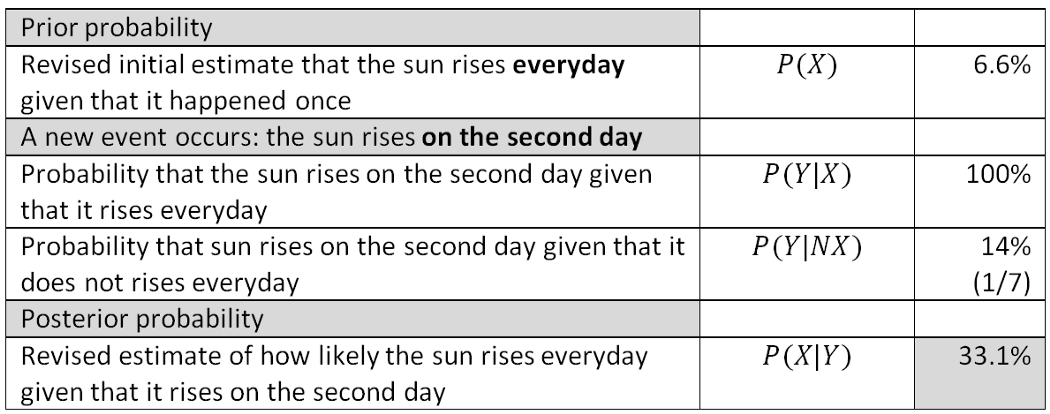
How Adam arrived at the conditional probability after the second sunrise

Upon observing the second sunrise, Adam becomes more convinced about his hypothesis, increasing his conditional probability from 6.6% to 33.1%. This process repeats times and times again, and even though it will never mathematically reach 100%, it later becomes a literal impossibility that the sun rises only by chance.

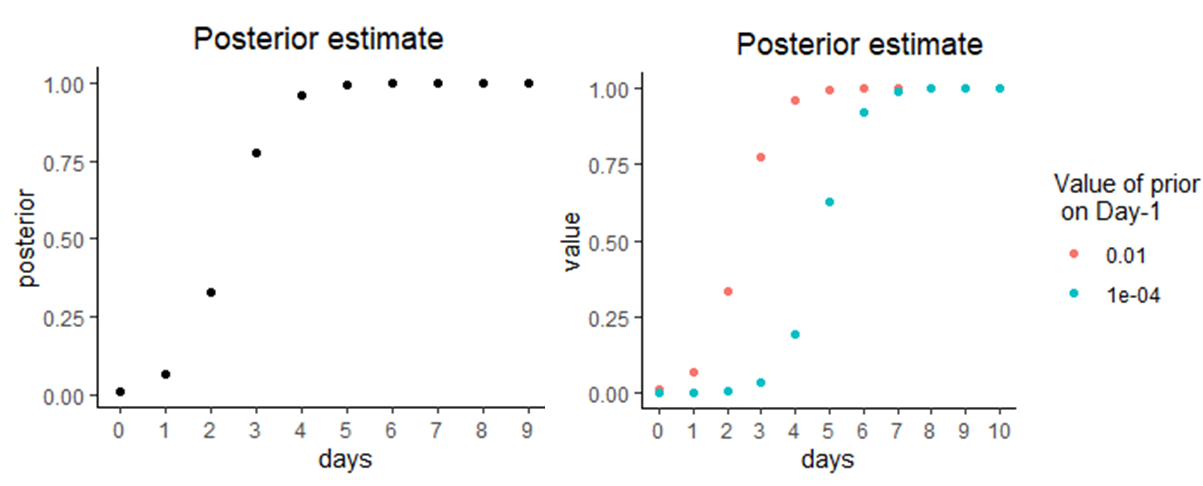
Left: the posterior conditional probability of the statement “The sun rises everyday” as Adam updates his belief daily. Right: Comparison between two different initial priors (1% vs 0.01%)

With some simple R code, I repeated the calculations above and illustrated how Adam updated his belief. You can find the source code here It takes him as few as 4 days to be more than 99% convinced in the daily occurrence of sunrise. Even if Adam is a lot more skeptical (as he should have been against the snake or Satan T.T) and assigned the initial belief at a mere 0.01%, it still would take only 7 days to convince him.

2. Bayes’ Theorem and the God of Miracles:

In this section, I will simplify the discussion (a.k.a outright cheating): instead of examining the probabilistic argument that God exists, we will focus on a narrow, but no less interesting topic: can we believe in Miracles?

There are 3 reasons why I decided to do so:

The rationality of Miracles, commonly defined as “a violation of the law of nature,” has been a hot subject of philosophical contention.
Theologically and philosophically speaking, there have been many arguments for the direct link between the existence of Miracles and the Deity himself, so we are not quite far from there.
Once you have seen the principle, it is relatively easy to replicate the same argument w.r.t the existence of God.

Can we believe in the existence of Miracles based on people’s testimonies?

For David Hume — a famous Scottish philosopher, answer is a resounding “NO”:

That no testimony is sufficient to establish a miracle, unless the testimony be of such a kind, that its falsehood would be more miraculous, than the fact, which it endeavors to establish^[2]

Now that was confusing. There are many ways we could try to read it, but one of the most interesting (and popular) interpretation was Bayesian in nature.

Let’s set up some definition of events: a particular miracle happens ($M$ and a record of testimony for such miracle ($T$). We can use the same Bayes’ framework to construct the conditional probability that a miracle really happens given some testimony.

$$P(M|T) = \frac{P(T|M)P(M)}{P(T|M)P(M) + P(T|M^C)P(M^C)}$$

To read Hume, we need to make the simplifying approximations that $P(T|M) \approx P(M^C)$ , since both terms are close to 1. This will allow us to simply the expression to:

$$P(M|T) \approx \frac{P(M)}{P(M) + P(T|M^C)}$$

with a little bit of algebra, it is easy for us to see that $P(M|T) > 0.5$ if and only if $P(M) > P(T|M^C)$. And this is exactly what Hume means when he says that “the falsehood [$P(T|M^C)$] is more miraculous [smaller than] than the fact it tries to establish [$P(M)$].”

This is based on this exact argument that Hume responds to testimonies of the resurrection of Jesus:

When anyone tells me, that he saw a dead man restored to life, I immediately consider with myself, whether it be more probable, that this person should either deceive or be deceived, or that the fact, which he relates, should really have happened. I weigh the one miracle against the other; and according to the superiority, which I discover, I pronounce my decision, and always reject the greater miracle^[2].

The basis for his skepticism is that the probability of the resurrection P(M=resurrection) is significantly smaller than the probability of false testimonies P(testimony|no resurrection), which makes P(resurrection|testimony ) < 0.5. More generally, it is next to impossible to find cases in which $P(M) > P(T|M^C)$, and so we can never reliably associate a testimony with a cause — an actual miracle.

Left: David Hume. Right: Thomas Bayes — although many argues that it is not his portrait. Source: Wikipedia

I hope you can see the unsettling nature of Hume’s argument. Hume believed that we can never be certain about anything based solely on traditional beliefs, coexistence, or testimony. Taking this idea even further, in a few essays that sent an intellectual shock across the 1700-Europe, Hume directed an attack at one of the oldest argument for God’s existence, the teleological argument. That is, an intelligent creator is evidenced by the perceived deliberate design in the natural world and God is the First Cause of everything. By establishing that our induction can seldom be reliable and criticizing cause-effect concepts altogether, Hume undermined the very core tenets of Christian’s beliefs.

3. What Hume was missing:

The issue with this line of interpretation is that it fails to recognize many of the other considerations that human account for when we hear a testimony of miracles:

How many independent testimonies are there? According to the Gospel of John, there are at least 3 testimonies to the Empty tomb (Mary Magdalene, Simon Peter and “another disciple whom Jesus loved”)
The bigger question is: How many different miracles we need before we can establish the conditional probability of God’s existence?

Let us consider the case of multiple independent testimonies. A good way to think about it is to use Bayesian updating for each new person arrives and testifies. And so, we arrive at a result very similar to the sunrise example in the previous part — where the conditional probability converges to 1.

Here, let tackle the problem a little bit differently and try to exploit the independence assumption to simplify the math. Assuming that for a particular miracle $M$, a person $i$ will give a testimony $T_i$, we set up the conditional probability for the miracle given $n$ testimonies:

$$P(M|T_1, T_2,..., T_n) = \frac{P(T_1, T_2,..., T_n|M)P(M)}{P(T_1, T_2,..., T_n|M)P(M) + P(T_1, T_2, ..., T_n|M^C)P(M^C)}$$

Now, assuming that these testimonies are independent (which is a huge assumption — and we know this is not true in the story from John's Gospel) and has probability of being truthful $p$ or $P(T|M) = p$ and probability of being fake $q$ or $P(T|M^C) = q$, we can simply the terms as follows:

This allows us to simplify the conditional probability into:

$$\begin{array}{lcl} P(M|T_1, T_2,..., T_n) & = & \frac{P(M) \times p^n}{P(M) \times p^n + P(M^C) \times q^n} \\ & = & \frac{1}{1 + \frac{P(M^C)}{P(M)} \times (\frac{q}{n})^n} \end{array} $$

Normally, we would assume $q < p$ (i.e, it is more likely that people testify when they see a miracle than to fake when they did not), which means that as $n \longrightarrow 0, (q/p)^n \longrightarrow 0$, and the conditional probability approaches 1.

Another very cool fact is, even though $P(M)$ can be very small, you can always find n that makes the conditional probability $> 0.5$

The point is, whether you employ Bayesian updating or take advantage of independence assumption, Hume’s (already questionable) contention that no individual testimony can be reliable does not preclude the combined testimonies from being so.

What I have introduced so far is the basic construction used to make probabilistic argument for theological matters. In fact, Richard Swinburne did plug in a number and arrive at the probability of Resurrection of a whooping 97%^[3]. We can easily extend this framework to include the “existence of God.” For example, where $G$ stands for “God exists” (where “God” is conceived classically as an eternal being of maximal power, knowledge, and goodness who created the universe),we can make the assumptions that $P(M|G) \gg P(M|G^C)$ and that either $P(M|G^C)=0$ or $P(M|G^C)\approx 0$ (if miracles are strictly the prerogative of God) and the same sort of discussion follows.

The problem with this type of probabilistic argument is that even if the Mathematics convince you completely, depending on the assumptions and the set-up, you can arrive at completely contrasting conclusions.

However, this post is meant to appreciate how intricately beautiful Bayes system is. A skeptic, David Hume would argue that drawing any causal inferences from past experience is futile because we need to extrapolate the past into the future, which we cannot be sure of. On the other hand, Bayes — who treats rationality as probabilistic in nature, would tell Hume not to blame nature if one is too meek to comprehend it; if you step out of your skeptical shell and boldly make some predictions about its behavior, perhaps you will get a little closer to the truth.

The entire R script for this article can be found at my Github page.

[1] Mcgrayne, Sharon Bertsch.The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy. Yale University Press, 2011

[2] Hume, An Enquiry concerning Human Understanding X, i, 86

[3] Swinburne, Richard, The Resurrection of God Incarnate, Oxford University Press, 2003